【数学】中1生 1学期中間テストで100点目指す! ~正の数・負の数~

数学の最も基本になるのが『正の数・負の数』です。中学に入り、最初に学ぶ単元で、これまでの算数にはない新しい考え方なので、意外とつまづいてしまう新中学1年生の生徒さんも多いようです。
こちらでも詳細お伝えしています。
今回はそんな『正の数・負の数』についてご紹介します。
要点のまとめ!
『正の数・負の数』要点のまとめ
1)0より大きい数が正の数、0より小さい数が負の数
2)数直線上で、ある数を示す点と原点との距離が絶対値
3)同じ数を複数かけたものが累乗
4)ある条件にあてはまる数字全体が集合
1)0より大きい数が正の数、0より小さい数が負の数
小学生までで使っていた0より大きな数字を正の数、そして新しく出てくるのが0より小さい数「負の数」です。数字の前に「ー(マイナス)」をつけて表します。
 ハカセ
ハカセ
「0」は正の数でも負の数でもないぞ。
整数は、正の整数・0・負の整数に分けられます。この正の整数のことを、特に自然数といいます。
2)数直線上で、ある数を示す点と原点との距離が絶対値
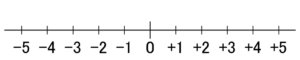
図のように、数字を直線上に示したものを数直線といいます。0を原点として、右側が正の数、左側が負の数になります。そして、0(原点)からある数までの距離が「絶対値」になります。
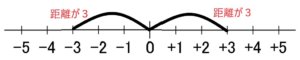
この図のように、0(原点)から距離が3の数字は正の数「+3」と負の数「-3」の二つがあることがわかります。つまり絶対値が3になる数字は+3と-3の二つです。
3)同じ数を複数かけたものが累乗
「5×5」のように同じ数字をかけたものを累乗と言います。式としては、

のように右上に何回かけているのを示すように書きます。この右上の何回かけているかを示す小さく表記した数字を「指数」と言います。
累乗の計算でよくやってしまう間違い
例えば、本来「5×5」である「52」を「5×2」とよく間違えることがあります。この違いに注意しておきましょう。
52=5×5=25
5×2=10
4)ある条件にあてはまる数字全体が集合
あまり難しく考えずに、同じ仲間のひとくくりを「集合」と呼ぶということです。例えば、「自然数全体」などのような、ある条件にあてはまる数字のまとまり全体のことです。
確認ポイント!
次に、正の数・負の数の単元での確認ポイントです!
▶ 正の数・負の数の加法(足し算)
同符号の加法 : 絶対値の和に、共通の符号をつける
<例> (-3)+(-5)=
(-3)の絶対値 → 3
(-5)の絶対値 → 5
絶対値の和は、3+5=8
共通の符号は「-」
よって、答えは「-8」
異符号の加法 : 絶対値の差に、絶対値が大きい方の符号をつける
<例> (-9)+(-3)=
(-9)の絶対値 → 9
(-3)の絶対値 → 3
絶対値の差は、9-3=6
絶対値が大きいのは「-9」で、その符号は「-」
よって、答えは「-6」
▶ かっこのはずし方
+( )の場合 : かっこの中の符号は変えない
<例> +(-5) → -5
-( )の場合 : かっこの中の符号を変える
<例> -(-5) → +5
▶ 逆数
2つの数字の積(かけ算の答え)が「1」になるとき、一方の数字を他方の数字の逆数と言います。この逆数は、苦手な生徒が多い「分数のわり算」で大活躍します。
分数のわり算は、逆数にしてかけ算に変える
<例> (-8)÷(-2/3)=
(-2/3)の逆数は(-3/2)
よって、
(-8)÷(-2/3)
=(-8)×(-3/2)
= 12
 ハカセ
ハカセ
逆数はあまり難しく考えず、「分数の分母と分子を入れ替える!」と覚えてしまっても大丈夫じゃ。
▶ 乗法・除法の計算
式の中に「̠-」が偶数個ある場合 : 積・商の符号は「+」
式の中に「̠-」が奇数個ある場合 : 積・商の符号は「-」
<例> (-3)×(-2)×(+5)=
式の中に「-」は偶数個 → 積の符号は「+」
数字の積は、3×2×5=30
よって、答えは「+30」
よく出る問題!
正の数・負の数の単元はほとんどが計算問題です。その計算問題で確認されているのが、四則混合問題の計算順序です。ここで、しっかりと計算順序を確認しておきましょう。
【絶対覚える】四則混合の計算順序
1)累乗の計算
2)かっこの中を計算
3)かけ算・わり算を左から順に計算
4)たし算・ひき算を左から順に計算
<例> 10+(-3)2×(6-8)=
①累乗の計算
(-3)2=(-3)×(-3)=(+9)
②かっこの中を計算
(6-8)=(-2)
ここまでで、問題の式は、10+(+9)×(-2)になります。
③かけ算・わり算を計算
(+9)×(-2)=(-18)
よって、問題の式は、10+(-18)になります。
④たし算・ひき算を計算
10+(-18)=(-8)
高校入試ではこう出る!
最後に、中学数学の入り口で学ぶ「正の数・負の数」がどのように高校入試で出題されるのかをご紹介します。まず、大事なことは、
正負の数の計算問題は、高校入試で必ず出題される
ということです。もちろん、入試のレベルによって出題のされ方は異なります。正負の計算だけで出題される場合、正負の数以外の単元との融合問題の一部として出題される場合など、その出題形式は様々です。しかし、中学数学の基礎中の基礎の単元ですので、すべての単元の土台になっているといっても過言ではありません。そういう意味でも必ず出題されている単元となります。
やや難易度の高い出題パターンとしても、先に紹介した四則混合問題の計算までです。要点を抑えたうえで、計算の順序・ルールを抑えておけば必ず得点できる得意単元にできるでしょう。
また、一見難しそうに表現されている問題でも、問題文をしっかり読めば、対処できます。
数学のおすすめの勉強法はコチラでも紹介しています。
→ 『中学生の教科別勉強法【数学】』
「正の数・負の数」を得意単元にするには、
こちらでも紹介しているように、数学で得点できるようにするために大事なことは、
1)解き方がわかる
2)正確に計算ができる
この二つです。そして、「正の数・負の数」の単元においては、「計算の正確性(計算力)」は特に大事になります。計算力UPのポイントはとにかく計算量です。
自学自習でしっかりと演習量を確保し、その理解度をチェックしながら進めることができる【LINE先生】がおすすめです。
新しい学びのカタチ【LINE先生】
・自学用教材でしっかり演習を確保
・定期的な課題提出で理解度をチェック

LINE先生専用教材をご用意します。自学で取り組むことを目的に用意された専用教材ですので、自分の好きなタイミング・場所で、しっかりと演習を確保することができます。

自分で学習するだけでなく、単元ごとに決まった課題があり、理解度をチェックできます。また、いつでもLINEで質問することもできるので、「わからない」を先延ばしにすることもなく、理解を深めていくことができます。
LINE先生の流れ
1)自学用教材を郵送で受け取る
2)個別カリキュラムに沿って演習
3)指定曜日までに提出用課題をLINEで提出
4)翌日中に添削内容を返信 → 復習する
5)わからない部分はLINEで随時質問!

友だち登録はこちらから


